关于有限体积法的一些认识

有限体积法的离散化

统一高斯公式

在场论中常用到的梯度公式，散度公式（高斯公式），旋度公式（斯托克斯公式公式）可以统一为如下形式，方便记忆: $\int_V\nabla \otimes A =\oint_{\partial V}\boldsymbol{n}\otimes AdS$

\[\nabla \otimes A =\lim\limits_{V\rightarrow 0}\frac{1}{V} \oint_{\partial V}\boldsymbol{n}\otimes AdS\]

当A为标量$\varphi$时，为梯度公式： $\int_V\nabla\varphi =\oint_{\partial V}\boldsymbol{n}\varphi dS$ 当A为矢量$\boldsymbol{F}$，$\otimes$为点乘时，此时为散度公式（即高斯公式）: $\int_V\nabla\cdot\boldsymbol{F} =\oint_{\partial V}\boldsymbol{n}\cdot\boldsymbol{F} dS$ 当A为矢量$\boldsymbol{F}$，$\otimes$为叉乘时，此时为旋度公式（即斯托克斯公式）: $\int_V\nabla\times\boldsymbol{F} =\oint_{\partial V}\boldsymbol{n}\times\boldsymbol{F} dS$ 另一种形式也是如此。

这三个公式能统一基于同样的物理含义：

控制体积内的物理量变化=从控制体积边界进出的物理量

下面可以开始推导了

标量

\[\int_V QdV\approx Q_c\Delta V\]

$Q_c$为控制体积中心的物理量，其精度为二阶。

梯度项离散

fluent里面对梯度项的处理有三种方式，可在Solution->Methods-> Spatial Discretization-> Gradient中选择，如图：

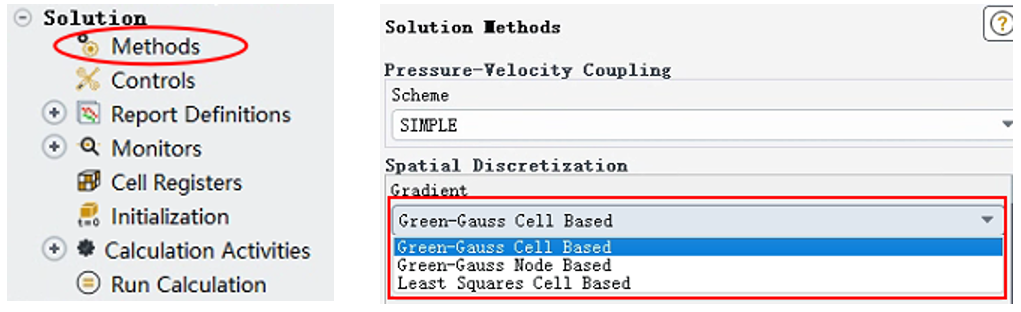
共三种方式，现简单介绍如下：

Creen-Guass Gradient

利用上面的公式： $\frac{\partial \varphi}{\partial x}=\lim\limits_{V\rightarrow 0}\frac{1}{V}\int_V\frac{\partial \varphi}{\partial x}dV=\lim\limits_{V\rightarrow 0}\frac{1}{V}\oint_{\partial V}\boldsymbol{n}_x\varphi dS\approx \frac{1}{\Delta V}\sum\limits_{i=1}^{n}\varphi_f A_i^x$

$\varphi_f$为网格界面的物理量，其需要通过周围网格的相应物理量重构（restriction）得到。

重构（restriction）和插值（interpolation）不是等同的，可以理解为：插值是重构的一种方法，但重构还有其他方法。

下面介绍fluent中使用的两种重构模板：

Creen-Guass Cell Based

或称格林-高斯梯度紧凑型模板（Creen-Guass gradient Compact Stencil）

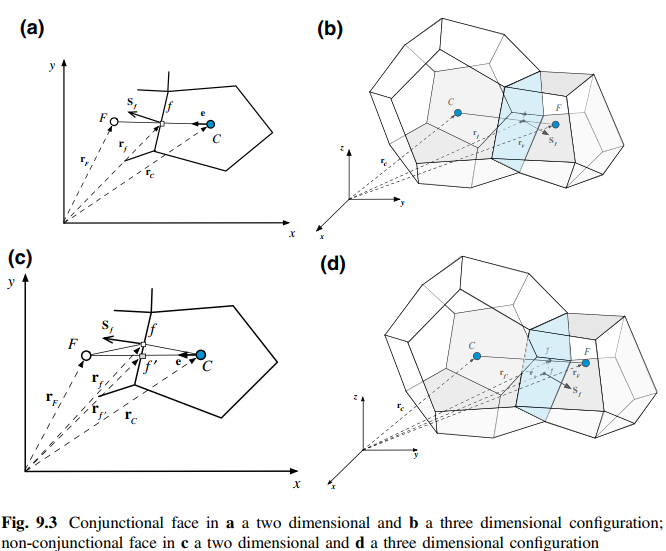
即使用两个共面单元的值取平均作为面上物理量的值，其有如下形式： $\phi_{f}=g_{C} \phi_{C}+\left(1-g_{C}\right) \phi_{F}$ 对于结构化网格，当$g_c$取0或1时，$\phi_f$为$\phi_F$或$\phi_F$ 其梯度项可化简为向前差分或向后差分。当然，这样做只有一阶精度，并不常用。

另一种$g_c$按如下取值： $g_{C}=\frac{\left\|\mathbf{r}_{F}-\mathbf{r}_{f}\right\|}{\left\|\mathbf{r}_{F}-\mathbf{r}_{C}\right\|}=\frac{d_{F f}}{d_{F C}}$ 此时对于结构化网格，此时 $\phi_{f}=\frac{\phi_{C}+\phi_{F}}{2}$ 其可化简为中心差分格式。当两个相邻单元中心的插值点$S_{f^\prime}$与面中心$S_f$重合时，具有二阶精度，如图(a)所示。其他情况下，需要先计算插值点$S_{f^\prime}$的值，再通过$S_{f^\prime}$的值估算$S_f$的值，如图(c)所示，修正公式如下： $\phi_f=\phi_{f^{\prime}}+(\nabla \phi)_{f^{\prime}} \cdot\left(\mathbf{r}_{f}-\mathbf{r}_{f^{\prime}}\right)$

\[\begin{aligned} \phi_{f} &=g_{C}\left\{\phi_{C}+(\nabla \phi)_{C} \cdot\left(\mathbf{r}_{f}-\mathbf{r}_{C}\right)\right\}+\left(1-g_{C}\right)\left\{\phi_{F}+(\nabla \phi)_{F} \cdot\left(\mathbf{r}_{f}-\mathbf{r}_{F}\right)\right\} \\ &=\phi_{f^{\prime}}+\underbrace{g_{C}(\nabla \phi)_{C} \cdot\left(\mathbf{r}_{f}-\mathbf{r}_{C}\right)+\left(1-g_{C}\right)(\nabla \phi)_{F} \cdot\left(\mathbf{r}_{f}-\mathbf{r}_{F}\right)}_{\text {correction }} \end{aligned}\]

插值点$S_{f^\prime}$有三种取法。

1.界面上的点。如上图(c)所示。

2.相邻单元中心连线的中点：

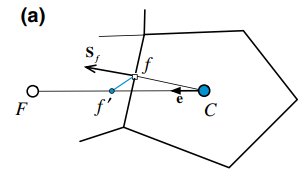
3.距f点最近的点。

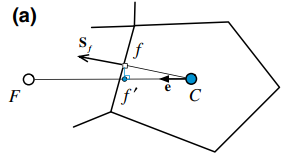
其有各自的算法，这里不再展开。

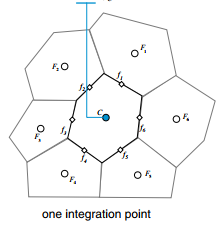
Creen-Guass Node Based

或称格林-高斯梯度扩展型模板（Creen-Guass Gradient Extended Stencil）

即通过界面两顶点的值取平均值得到。

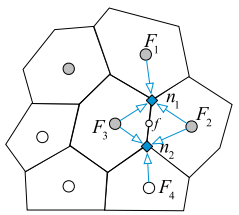$\phi_{n}=\frac{\sum\limits_{k=1}^{N B(n)} \frac{\phi_{F_{k}}}{\left\|\mathbf{r}_{n}-\mathbf{r}_{F_{k}}\right\|}}{\sum\limits_{k=1}^{N B(n)} \frac{1}{\left\|\mathbf{r}_{n}-\mathbf{r}_{F_{k}}\right\|}}$

\[\phi_{f}=\frac{\phi_{n_{1}}+\phi_{n_{2}}}{2}\]

如上图所示，先根据$F_1,F_2,F_3$的值求出$n_1$处的值，根据$F_2,F_3,F_4$的值求出$n_2$处的值，再得到$f$点的值。

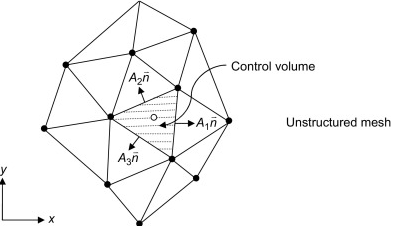
Least-Squares Gradient

最小二乘法梯度 Least-Squares Cell Based。

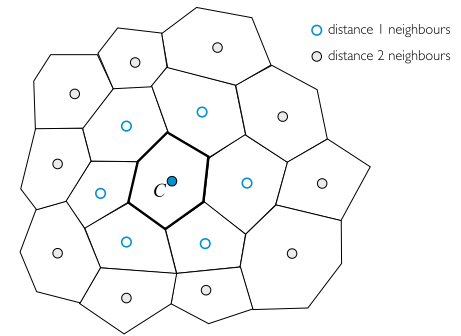
其梯度通过优化如下函数得到： $\begin{aligned} G_{C} &=\sum_{k=1}^{N B(C)}\left\{w_{k}\left[\phi_{F_{k}}-\left(\phi_{C}+\nabla \phi_{C} \cdot \mathbf{r}_{C F_{k}}\right)\right]^{2}\right\} \\ &=\sum_{k=1}^{N B(C)}\left\{w_{k}\left[\Delta \phi_{k}-\left(\Delta x_{k}\left(\frac{\partial \phi}{\partial x}\right)_{C}+\Delta y_{k}\left(\frac{\partial \phi}{\partial y}\right)_{C}+\Delta z_{k}\left(\frac{\partial \phi}{\partial z}\right)_{C}\right)\right]^{2}\right\} \end{aligned}$ 其中自变量为梯度的三个分量。即： $\frac{\partial G_{C}}{\partial\left(\frac{\partial \phi}{\partial x}\right)}=\frac{\partial G_{C}}{\partial\left(\frac{\partial \phi}{\partial y}\right)}=\frac{\partial G_{C}}{\partial\left(\frac{\partial \phi}{\partial z}\right)}=0$ 极值点的值即为$\nabla\phi_C$

该方法中最重要的是权重$w_k$的确认。以上方法至少有一阶精度（不详细描述了）。

小结

根据以上理论，可以对以上方法做一个小结。首先是计算开销，有

Green-Gause Cell Based < Least-Squares Cell Based < Green-Gause Node Based

但显然，Green-Gause Cell Based方法的精度对于网格质量要求较高，低质量网格显然是不能使用该方法的。

在面对复杂的工程问题时，不可避免的会碰到低质量网格，此时 Least-Squares Cell Based < Green-Gause Node Based 有着接近且较高的精度，故而通常采用Least-Squares Cell Based 方法。而对于网格质量很高的模型，可以选用Green-Gause Cell Based方法节省计算开销。

扩散项的离散

扩散项通常有如下形式： $-\nabla \cdot\left(\Gamma^{\phi} \nabla \phi\right)=Q$ 比如热量扩散方程，扩散项为 $-\nabla \cdot\left(\kappa \nabla T\right)=-\frac{\partial }{\partial x}(\kappa_{x} \frac{\partial T}{\partial x})-\frac{\partial }{\partial y}(\kappa_{y} \frac{\partial T}{\partial y})-\frac{\partial }{\partial z}(\kappa_{z} \frac{\partial T}{\partial z})$ 通常的处理方式为定义一个流， $\boldsymbol{J} =-\Gamma^{\phi} \nabla \phi,\quad Q = \nabla \boldsymbol{J}$ 比如根据傅里叶定律，有热流: $q = -\kappa\nabla T$ 根据上面对梯度的处理，进行两次离散处理。当然具体还有很多门道，这里暂时不再细说。

本文由 joe_zhouman 创作，采用知识共享署名4.0 国际许可协议进行许可
本站文章除注明转载/出处外，均为本站原创或翻译，转载前请务必署名
最后编辑时间为:2022-05-07 10:12:48