常用拉普拉斯变换及其性质
常用变换




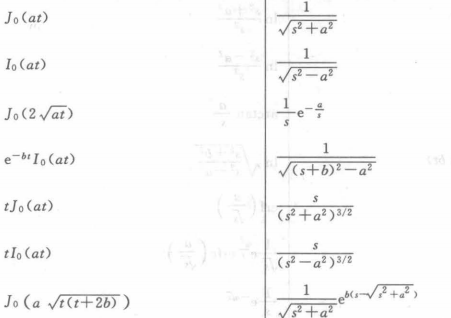
基本性质
线性
\(\mathscr{L}[\alpha f(t)+\beta g(t)]=\alpha F(s)+\beta G(s)\) \(\mathscr{L}^{-1}[\alpha F(s)+\beta G(s)]=\alpha f(t)+\beta g(t)\)
伸缩性
\[\mathscr{L}[f(a t)]=\frac{1}{a} F\left(\frac{s}{a}\right), a\gt 0\]微积分运算
若$\mathscr{L}[f(t)]=F(s)$
\[\mathscr{L}\left[f^{(n)}(t)\right]= s^{n} F(s)-s^{n-1} f(0)-s^{n-2} f^{\prime}(0)- \cdots-f^{(n-1)}(0)\]其中
\[f^{(k)}(0)=\lim _{t \rightarrow 0^{+}} f^{(k)}(t)\] \[F^{(n)}(s)=(-1)^{n} \mathscr{L}\left[t^{n} f(t)\right] .\] \[\mathscr{L}[\underbrace{\int_{0}^{t} \mathrm{~d} t \int_{0}^{t} \mathrm{~d} t \cdots \int_{0}^{t}}_{n \text { 次 }} f(t) \mathrm{d} t]=\frac{1}{s^{n}} F(s) .\] \[\underbrace{\int_{s}^{\infty} \mathrm{d} s \int_{s}^{\infty} \mathrm{d} s \cdots \int_{s}^{\infty} F(s) \mathrm{d} s=\mathscr{L}\left[\frac{f(t)}{t^{n}}\right] \text {. }}\]延时性
\[\mathscr{L}[f(t-\tau)]=\mathrm{e}^{-s \tau} F(s)\]位移性
\[\mathscr{L}\left[\mathrm{e}^{a t} f(t)\right]=F(s-a)\]周期函数
设 $f(t)$ 是 $[0, +\infty)$ 内以 $T$ 为周期的函数, 且 $f(t)$ 在一个周期内逐 段光滑, 则
\[\mathscr{L}[f(t)]=\frac{1}{1-\mathrm{e}^{-s T}} \int_{0}^{T} f(t) \mathrm{e}^{-s t} \mathrm{~d} t\]卷积
\[\mathscr{L}\left[f_{1}(t) * f_{2}(t)\right]=F_{1}(s) \cdot F_{2}(s)\]
本文由 joe_zhouman 创作,采用 知识共享署名4.0
国际许可协议进行许可
本站文章除注明转载/出处外,均为本站原创或翻译,转载前请务必署名
最后编辑时间为:2021-11-22 21:13:53
