正则系综
正则系综
通过参量N、V和T来定义的系综为正则系综
系统与热库
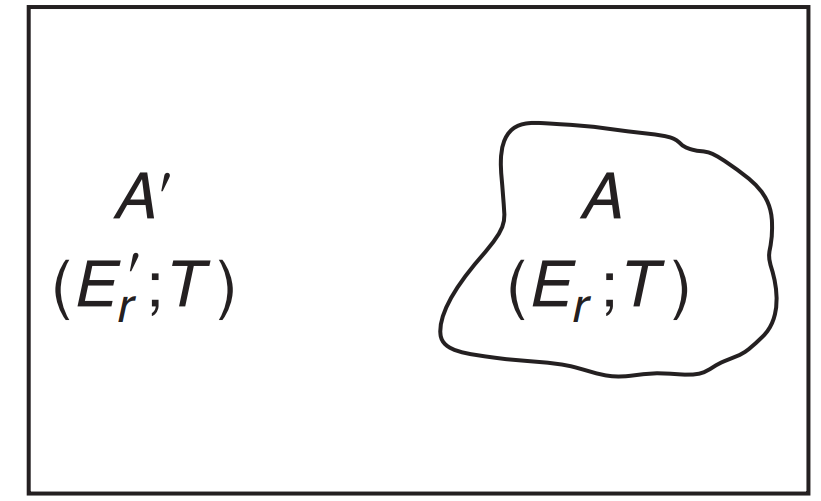
当对系统 $A$ 的状态已作规定之后, 而大热库 $A^{\prime}$ 却仍然还可以处在 与能量 $E_{r}^{\prime}$ 相容的大量状态中的任意一个. 处于某一能量的配分数越大, 处于该能量的概率越大
\[P_{r} \propto \Omega^{\prime}\left(E_{r}^{\prime}\right) \equiv \Omega^{\prime}\left(E^{(0)}-E_{r}\right)\] \[\ln \Omega^{\prime}\left(E_{r}^{\prime}\right) = \ln \Omega^{\prime}\left(E^{(0)}\right)+\left( \frac{\partial \ln \Omega^{\prime}}{\partial E^{\prime}} \right)_{E^{\prime}=E^{(0)}}\left(E_{r}^{\prime}-E^{(0)} \right)+\cdots \simeq \text { const }-\beta^{\prime} E_{r},\] \[P_{r} \propto \exp \left(-\beta E_{r}\right)\] \[P_{r}=\frac{\exp \left(-\beta E_{r}\right)}{\sum_{r} \exp \left(-\beta E_{r}\right)}\]此时$P_r$与热库性质无关。
正则系综中的系统
$n_{r}$ 表示在任意时刻 $t$ 具有能量为 $E_{r}$ 的系统的数目, 则这些数的集合 $n_{i}$ 必须满足以下这些明显的条件
\[\left.\begin{array}{l} \sum_{r} n_{r}=\mathcal{N} \\ \sum_{r} n_{r} E_{r}=\boldsymbol{\epsilon}=\mathcal{N} U, \end{array}\right\}\]满足上面关系的分布有很多,同时,每一个分布分配给系综中不同的系统,会得到不同的分布,这是一个组合问题。
\[W\left\{n_{r}\right\}=\frac{\mathscr{N}!}{\Pi_rn_i!}\]$W_r$越大,处于该状态的系统数越多,则系综处于这一状态的概率越大。
\[\left\langle n_{r}\right\rangle=\frac{\sum_{\left\{n_{r}\right\}}^{\prime} n_{r} W\left\{n_{r}\right\}}{\sum_{\left\{n_{r}\right\}}^{\prime} W\left\{n_{r}\right\}}\]最可几值推导
\[\ln W=\ln \left(\mathscr{N}!\right)-\sum_{r} \ln \left(n_{r !}\right)\]根据斯特林公式
\[\ln W=\mathscr{N} \ln \mathscr{N}-\sum_{r} n_r \ln n_{r}\]同时要满足上面的约束方程,按拉格朗日算子法,即求以下方程$V(n,\alpha,\beta)$的极值:
\[V=\ln W+\alpha\sum_rn_r+\beta\sum_rE_rn_r\]固有
\[\frac{\partial V}{\partial n_r}=-(\ln n_r+1)+\alpha+\beta E_r=0\] \[n_{r}^{*}=C \exp \left(-\beta E_{r}\right)\]回代到约束方程
\[\mathcal{N}=C\sum_{r} \exp \left(-\beta E_{r}\right)\] \[\epsilon=C\sum_rE_r\exp \left(-\beta E_{r}\right)\] \[\frac{n_{r}^{*}}{\mathcal{N}}=\frac{\exp \left(-\beta E_{r}\right)}{\sum_{r} \exp \left(-\beta E_{r}\right)}\] \[\frac{\epsilon}{\mathcal{N}}=U=\frac{\sum_{r} E_{r} \exp \left(-\beta E_{r}\right)}{\sum_{r} \exp \left(-\beta E_{r}\right)}\]平均值法
以后再理解,现在看上去还用不到。
统计量的物理意义
\[P_{r} \equiv \frac{\left\langle n_{r}\right\rangle}{\mathcal{N}}=\frac{\exp \left(-\beta E_{r}\right)}{\sum_{r} \exp \left(-\beta E_{r}\right)}\] \[U=\frac{\sum_{r} E_{r} \exp \left(-\beta E_{r}\right)}{\sum_{r} \exp \left(-\beta E_{r}\right)}=-\frac{\partial}{\partial \beta} \ln \left\{\sum_{r} \exp \left(-\beta E_{r}\right)\right\}\]考虑霍姆亥兹自由能$A$,$dA=-PdV-SdT+\mu dN$
\[U=A+T S=A-T\left(\frac{\partial A}{\partial T}\right)_{N, V}=-T^{2}\left[\frac{\partial}{\partial T}\left(\frac{A}{T}\right)\right]_{N, V}=\left[\frac{\partial(A / T)}{\partial(1 / T)}\right]_{N, V},\] \[\beta=\frac{1}{k T}, \quad \ln \left\{\sum_{r} \exp \left(-\beta E_{r}\right)\right\}=-\frac{A}{k T}\] \[A(N, V, T)=-k T \ln Q_{N}(V, T)=-kT\sum_{r} \exp \left(-E_{r} / k T\right)\]$Q_N$称为配分函数。 热力学量均可从以上关系中推导而出。
\[S=-k\left\langle\ln P_{r}\right\rangle=-k \sum_{r} P_{r} \ln P_{r}\]简并的配分函数
对于能级$E_i$有$g_i$个简并态
\[Q_{N}(V, T)=\sum_{i} g_{i} \exp \left(-\beta E_{i}\right)\] \[P_{i}=\frac{g_{i} \exp \left(-\beta E_{i}\right)}{\sum_{i} g_{i} \exp \left(-\beta E_{i}\right)}\]每个能量对应的简并数极大,故而可以过渡到连续谱
\[Q_{N}(V, T)=\int_{0}^{\infty} e^{-\beta E} g(E) d E .\] \[\langle f\rangle \equiv \sum_{i} f_{i} P_{i}=\frac{\sum_{i} f\left(E_{i}\right) g_{i} e^{-\beta E_{i}}}{\sum_{i} g_{i} e^{-\beta E_{i}}} \rightarrow \frac{\int_{0}^{\infty} f(E) e^{-\beta E} g(E) d E}{\int_{0}^{\infty} e^{-\beta E} g(E) d E} .\]可以看到,配分函数$Q_\beta$是态密度$g(E)$的拉普拉斯变换。
相空间与量子态
\[\langle f\rangle=\frac{\int f(q, p) \rho(q, p) d^{3 N} q d^{3 N} p}{\int \rho(q, p) d^{3 N} q d^{3 N} p}\] \[\rho(q, p) \propto \exp \{-\beta H(q, p)\}\] \[\langle f\rangle=\frac{\int f(q, p) \exp (-\beta H) d \omega}{\int \exp (-\beta H) d \omega}\]考虑到不确定性原理及粒子的不可分辨性,体积元内对应的量子态数有:
\[\frac{d \omega}{N_{!} h^{3 N}}\] \[Q_{N}(V, T)=\frac{1}{N ! h^{3 N}} \int e^{-\beta H(q, p)} d \omega\]涨落
正则系综和微正则系综的表达式等价性。
\[U \equiv\langle E\rangle=\frac{\sum_{r} E_{r} g_{r} \exp \left(-\beta E_{r}\right)}{\sum_{r} g_{r} \exp \left(-\beta E_{r}\right)} .\] \[\frac{\partial U}{\partial \beta} =-\frac{\sum_{r} E_{r}^{2} \exp \left(-\beta E_{r}\right)}{\sum_{r} \exp \left(-\beta E_{r}\right)}+ \frac{\left[\sum_{r} E_{r} \exp \left(-\beta E_{r}\right)\right]^{2}}{\left[\sum_{r} \exp \left(-\beta E_{r}\right)\right]^{2}} =-\left\langle E^{2}\right\rangle+\langle E\rangle^{2}\] \[\left\langle(\Delta E)^{2}\right\rangle \equiv\left\langle E^{2}\right\rangle-\langle E\rangle^{2}=-\left(\frac{\partial U}{\partial \beta}\right)=k T^{2}\left(\frac{\partial U}{\partial T}\right)=k T^{2} C_{V}\] \[\frac{\sqrt{\left\langle(\Delta E)^{2}\right\rangle}}{\langle E\rangle}=\frac{\sqrt{ k T^{2} C_{V}}}{U}\]当$N\rightarrow\infty$时,相对涨落可以忽略不计。近似于处于平均能量的微正则系综。
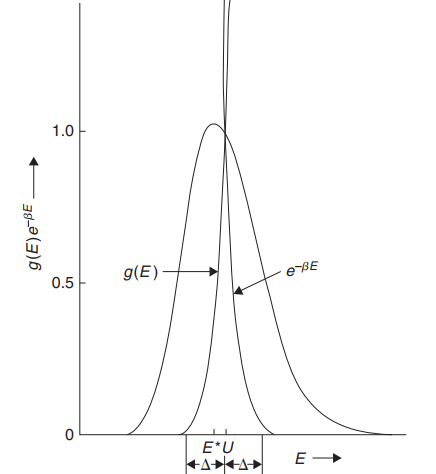
\[P(E) \propto \exp (-\beta E) g(E)\]P最大的即为最可能处于的状态
\[\frac{\partial}{\partial E}\left\{e^{-\beta E} g(E)\right\}=0\] \[\frac{\partial \ln g(E)}{\partial E}=\beta\]而
\[S=k \ln g \quad \text { and } \quad\left(\frac{\partial S(E)}{\partial E}\right)_{E=U}=\frac{1}{T}=k \beta,\]则平衡态能量$E^{*}=U$
系统最可能处于的状态与其平均状态相同。
将P在U附近展开至二阶项(一阶项为0)
\[\ln[e^{-\beta E}g(E)]=-\beta(U-T S)-\frac{1}{2 k T^{2} C_{V}}(E-U)^{2}+\cdots,\] \[P(E) \propto e^{-\beta E} g(E) \simeq e^{-\beta(U-T S)} \exp \left\{-\frac{(E-U)^{2}}{2 k T^{2} C_{V}}\right\}\]期望一正态分布。当$N\rightarrow\infty$时,其趋于一个$\delta$函数。
本文由 joe_zhouman 创作,采用 知识共享署名4.0
国际许可协议进行许可
本站文章除注明转载/出处外,均为本站原创或翻译,转载前请务必署名
最后编辑时间为:2021-12-05 00:15:38
