谐振子模型的统计力学推演
微正则系综
\[H(q, p)=\frac{1}{2} k q^{2}+\frac{1}{2 m} p^{2}\] \[q=A \cos (\omega t+\varphi), \quad p=-m \omega A \sin (\omega t+\varphi)\] \[\omega=\sqrt{k / m}\] \[E=\frac{1}{2} m \omega^{2} A^{2}\]其在相空间的轨迹为
\[\frac{q^{2}}{\left(2 E / m \omega^{2}\right)}+\frac{p^{2}}{(2 m E)}=1\]能量邻域的体积为
\[\frac{2 \pi}{\omega} \Delta\]能量本征值
\[E_{n}=\left(n+\frac{1}{2}\right) \hbar \omega ; \quad n=0,1,2, \cdots\]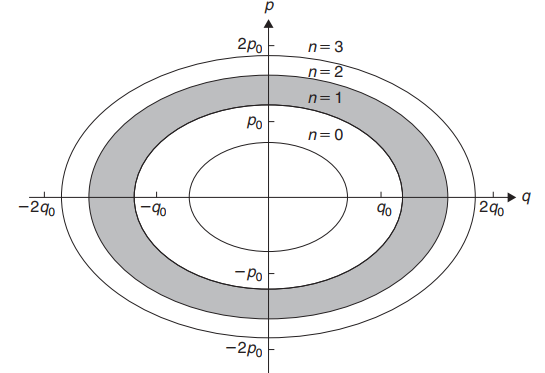
正则系综
经典效应
\(\begin{aligned} Q_{1}(\beta)=\int e^{-\beta H}d\omega &=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \exp \left\{-\beta\left(\frac{1}{2} m \omega^{2} q^{2}+\frac{1}{2 m} p^{2}\right)\right\} \frac{d q d p}{h} \\ &=\frac{1}{h}\left(\frac{2 \pi}{\beta m \omega^{2}}\right)^{1 / 2}\left(\frac{2 \pi m}{\beta}\right)^{1 / 2}=\frac{1}{\beta \hbar \omega}=\frac{k T}{\hbar \omega}, \end{aligned}\)
谐振子是可分辨的,不是粒子或准粒子,而是系统的能级
\[Q_{N}(\beta)=\left[Q_{1}(\beta)\right]^{N}=(\beta \hbar \omega)^{-N}=\left(\frac{k T}{\hbar \omega}\right)^{N}\] \[A \equiv-k T \ln Q_{N}=N k T \ln \left(\frac{\hbar \omega}{k T}\right)\] \[\mu=k T \ln \left(\frac{\hbar \omega}{k T}\right)\] \[P=0\] \[S=N k\left[\ln \left(\frac{k T}{\hbar \omega}\right)+1\right]\] \[U=N k T\] \[C_{P}=C_{V}=N k\]态密度
\[g(E)=\frac{1}{(\hbar \omega)^{N}} \frac{1}{2 \pi i} \int_{\beta^{\prime}-i \infty}^{\beta^{\prime}+i \infty} \frac{e^{\beta E}}{\beta^{N}} d \beta \quad\left(\beta^{\prime}>0\right)\] \[g(E)=\left\{\begin{array}{ll} \frac{1}{(\hbar \omega)^{N}} \frac{E^{N-1}}{(N-1) !} & \text { for } \quad E \geq 0 \\ 0 & \text { for } \quad E \leq 0 \end{array}\right.\] \[S(N, E)=k \ln g(E) \approx N k\left[\ln \left(\frac{E}{N \hbar \omega}\right)+1\right]\] \[T=\left(\frac{\partial S}{\partial E}\right)_{N}^{-1}=\frac{E}{N k}\]量子效应
\[\varepsilon_{n}=\left(n+\frac{1}{2}\right) \hbar \omega ; \quad n=0,1,2, \ldots\] \[Q_{1}(\beta) =\sum_{n=0}^{\infty} e^{-\beta(n+1 / 2) \hbar \omega}=\frac{\exp \left(-\frac{1}{2} \beta \hbar \omega\right)}{1-\exp (-\beta \hbar \omega)}\] \[Q_{N}(\beta) =\left[Q_{1}(\beta)\right]^{N} =e^{-(N / 2) \beta \hbar \omega}\left\{1-e^{-\beta \hbar \omega}\right\}^{-N}\] \[A=N\left[\frac{1}{2} \hbar \omega+k T \ln \left\{1-e^{-\beta \hbar \omega}\right\}\right],\] \[\mu =A / N ,P =0\] \[S =N k\left[\frac{\beta \hbar \omega}{e^{\beta \hbar \omega}-1}-\ln \left\{1-e^{-\beta \hbar \omega}\right\}\right]\]\(C_{P}=C_V =N k(\beta \hbar \omega)^{2} \frac{e^{\beta \hbar \omega}}{\left(e^{\beta \hbar \omega}-1\right)^{2}} .\) \(U=\frac{1}{2} N \hbar \omega \operatorname{coth}\left(\frac{1}{2} \beta \hbar \omega\right)=N\left[\frac{1}{2} \hbar \omega+\frac{\hbar \omega}{e^{\beta \hbar \omega}-1}\right]\)
此式不符合能量均分定理
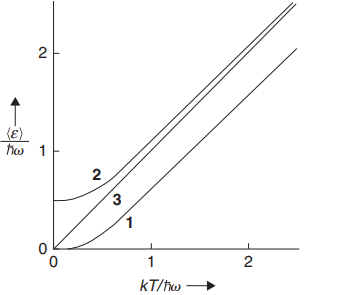
在高温的极限情兄下(此时热能 $k T$ 比能量子 $\hbar \omega$ 大得多), 每个振 子的平均能量趋向于均分值. 此处必须注意到, 如果没有零点能 $\frac{1}{2} \hbar \omega$ 的话, 平均能的极限值本来是 $\left(k T-\frac{1}{2} \hbar \omega\right)$, 而不是 $k T-$ 我们称这样的一个振子为普朗克振子.
\[g(E)=\sum_{R=0}^{\infty}\left(\begin{array}{c} N+R-1 \\ R \end{array}\right) \delta\left(E-\left\{R+\frac{1}{2} N\right\} \hbar \omega\right)\]当系统的能量 $E$ 具有分立值 $\left(R+\frac{1}{2} N\right) \hbar \omega$ (其中 $R=0,1,2 \cdots$ )之时, 则该系统可资用的状态数为 $(N+R-1) ! / R !(N-1) !$ 而对于其他的 $E$ 值, 根本没有任何可资用的状态。相当于把$R$个不可分辨量子,放到$N$个可分辨的能级之中,为一个组合问题。
巨正则系综
定域粒子系统,在某些方面可作为固体的近似。从数学上与谐振子类似。组成系统的微观实体相互可分辨 \(Q_{N}(V, T)=\left[Q_{1}(V, T)\right]^{N}\) 定域下单粒子配分函数与体积无关 \(Q_{1}(V, T)=\varphi(T)\)
\[\mathcal{Q}(z, V, T)=\sum_{N_{r}=0}^{\infty}[z \phi(T)]^{N_{r}}=[1-z \phi(T)]^{-1}\]量 $z \varphi(T)$ 必须保持小于 1 , 使得对 $N_{\text {r }}$ 的求和仍然是收敛的. \(P \equiv \frac{k T}{V} q(z, T)=-\frac{k T}{V} \ln \{1-z \phi(T)\}\)
\[N=\frac{z \phi(T)}{1-z \phi(T)}\] \[U=\frac{z k T^{2} \phi^{\prime}(T)}{1-z \phi(T)}\] \[A=N k T \ln z+k T \ln \{1-z \phi(T)\}\] \[S=-N k \ln z-k \ln \{1-z \phi(T)\}+\frac{z k T \phi^{\prime}(T)}{1-z \phi(T)}\] \[z \phi(T)=\frac{N}{N+1} \simeq 1-\frac{1}{N} \quad(N \gg 1)\] \[U / N=k T^{2} \phi^{\prime}(T) / \phi(T)\] \[A / N=-k T \ln \phi(T)+O\left(\frac{\ln N}{N}\right)\] \[S / N k=\ln \phi(T)+T \phi^{\prime}(T) / \phi(T)+O\left(\frac{\ln N}{N}\right)\]对一维量子谐振子 \(\phi(T)=[2 \sinh (\hbar \omega / 2 k T)]^{-1}\) 对一维经典谐振子 \(\phi(T)=k T / \hbar \omega\)
固汽平衡
\[z_{g}=\frac{N_{g}}{V_{g} f(T)}\] \[z_{s} \simeq \frac{1}{\phi(T)}\]封闭体积下,系统处于平衡状态,气固两相化学势相等,逸度相等$z_g=z_s$ \(N_{g} / V_{g}=f(T) / \phi(T)\) 此式给出固相形成的条件 \(N \geqslant V \frac{f(T)}{\varphi(T)}\) $N$为总粒子数。
气相密度很低,温度很高,则 \(P_v=\frac{N_{g}}{V_{g}} k T=k T \frac{f(T)}{\varphi(T)}\) 气相为单原子气体 \(f(T)=(2 \pi m k T)^{3 / 2} / h^{3}\) 固相为爱因斯坦模型下的三维谐振子 \(\phi(T)=[2 \sinh (h \omega / 2 k T)]^{-3} .\) 粒子由固相到自由相需要分离能$\varepsilon$.气相与固相之间的能量相差一个因子,在严格考虑下不能忽略。 \(P_{v}=k T\left(\frac{2 \pi m k T}{h^{2}}\right)^{3 / 2}[2 \sinh (\hbar \omega / 2 k T)]^{3} e^{-\varepsilon / k T} .\)
本文由 joe_zhouman 创作,采用 知识共享署名4.0
国际许可协议进行许可
本站文章除注明转载/出处外,均为本站原创或翻译,转载前请务必署名
最后编辑时间为:2021-12-05 00:20:01
