理想气体的统计力学推导
理想气体
对于理想气体,每个分子均看做质点,则
\[\Omega(N, E, V) \propto V^{N}\] \[\frac{P}{T} \equiv k\left(\frac{\partial \ln \Omega(N, E, V)}{\partial V}\right)_{N, E}=k \frac{N}{V}\] \[PV = nkT\]关于气体分子不在可以视作质点时的推导参见经典气体
在边长为L的方箱内,粒子的波函数接近于三维的无限深势阱,对应的能量本征值为
\[\varepsilon\left(n_{x}, n_{y}, n_{z}\right)=\frac{h^{2}}{8 m L^{2}}\left(n_{x}^{2}+n_{y}^{2}+n_{z}^{2}\right) ; \quad n_{x}, n_{y}, n_{z}=1, 2, 3, \ldots\]$\Omega(N, V, E)$为以下方程正整数解的个数:
\[\sum_{r=1}^{3 N} n_{r}^{2}=\frac{8 m V^{2 / 3} E}{h^{2}}=E^{*}\]故而
\[S(N, V, E) \equiv S\left(N, V^{2 / 3} E\right)\]绝热过程,N和S不变,则
\[V^{2 / 3} E=Const\]$\Omega(N, V, E)$, 或更确切地说, $\Omega_{N}(E^{\star})$, 就等于处在半径为 $\sqrt{E^{\star}}$ 的 $3 N$ 维球面上正整数的阵点数。
$\Sigma_{N}(E^{\star})$ 定义为处于半径为 $\sqrt{E^{\star}}$ 的 $3 N$ 维球面内的正整数阵点数,则
\[\Sigma(N, V, E)=\sum_{E^{\prime} \leq E} \Omega\left(N, V, E^{\prime}\right)\] \[\lim _{\varepsilon^{*} \rightarrow \infty} \frac{\Sigma_{1}\left(\varepsilon^{*}\right)}{(\pi / 6) \varepsilon^{* 3 / 2}}=1\]去除含0坐标的点
\[\Sigma_{1}\left(\varepsilon^{*}\right) \approx \frac{\pi}{6} \varepsilon^{* 3 / 2}-\frac{3 \pi}{8} \varepsilon^{*}\]加上所有含0坐标点
\[\Sigma_{1}^{\prime}\left(\varepsilon^{*}\right) \approx \frac{\pi}{6} \varepsilon^{* 3 / 2}+\frac{3 \pi}{8} \varepsilon^{*}\]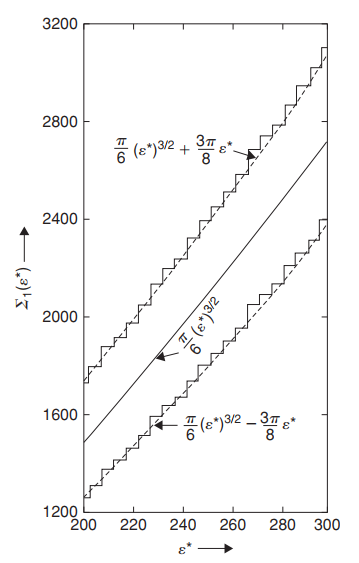
故
\[\ln \Sigma(N, V, E) \approx N \ln \left[\frac{V}{h^{3}}\left(\frac{4 \pi m E}{3 N}\right)^{3 / 2}\right]+\frac{3}{2} N\]根据不确定度原理,及测量误差的影响,我们难以获得精确处于$E$的能量态,而是位于$E-\Delta/2$ 和$E+\Delta/2$之间的态。并有$\Delta \ll E$,则这一范围内的微观态有:
\[\Gamma(N, V, E ; \Delta) \simeq \frac{\partial \Sigma(N, V, E)}{\partial E} \Delta \approx \frac{3 N}{2} \frac{\Delta}{E} \Sigma(N, V, E),\] \[\ln \Gamma(N, V, E ; \Delta) \approx N \ln \left[\frac{V}{h^{3}}\left(\frac{4 \pi m E}{3 N}\right)^{3 / 2}\right]+\frac{3}{2} N+\left\{\ln \left(\frac{3 N}{2}\right)+\ln \left(\frac{\Delta}{E}\right)\right\}\]而现在有$N\gg 1$,$\Delta \ll E$,故而大括号内的项可以忽略不计。
\[\ln \Gamma \approx \ln \Sigma \approx N \ln \left[\frac{V}{h^{3}}\left(\frac{4 \pi m E}{3 N}\right)^{3 / 2}\right]+\frac{3}{2} N\]$E$的领域的配容数与从0到$E$的配容数的总和相差无几,故而对配容数影响的主要因素其实就是其领域内的配容数。
吉布斯佯谬
\[S(N, V, E)=kln \Gamma=N k \ln \left[\frac{V}{h^{3}}\left(\frac{4 \pi m E}{3 N}\right)^{3 / 2}\right]+\frac{3}{2} N k\]以上公式中,$S$不是广延量。对配分函数除以$N!$,对于$S$来说,其减去$lnN!$。在根据斯特林公式,即可得到下式:
\[\begin{aligned} S(N, V, E) &=N k \ln \left[\frac{V}{N h^{3}}\left(\frac{4 \pi m E}{3 N}\right)^{3 / 2}\right]+\frac{5}{2} N k \\ &=N k \ln \left(\frac{V}{N}\right)+\frac{3}{2} N k\left\{\frac{5}{3}+\ln \left(\frac{2 \pi m k T}{h^{2}}\right)\right\} \end{aligned}\]粒子全同且不可分辨。相当于组合而不是排列。故而相差一个因子:($N!/\Pi n_i!$)。除以$N!$在所有粒子能量都不相同是是完全正确的 但在其他情况有些问题,但在经典极限下正确度足够了。考虑更详细的因子,则进入量子统计物理的领域。
当$P(n_i>1)\rightarrow 0$时,这样方法越来越接近实际。可以通过充分高的温度及充分低的密度来实现这一情况。 故而统计力学的经典极限可表示为$\left<n\right>\ll 1$
物理量的推导
\[T=\left(\frac{\partial E}{\partial S}\right)_{N, \nabla}=\frac{2}{3} \frac{E}{N k}\] \[E=N\left(\frac{3}{2} k T\right)=n\left(\frac{3}{2} R T\right)\] \[C_{V}=\left(\frac{\partial E}{\partial T}\right)_{N, V}=\frac{3}{2} N k=\frac{3}{2} n R\] \[P=-\left(\frac{\partial E}{\partial V}\right)_{N, S}=\frac{2}{3} \frac{E}{V}\] \[P=\frac{N k T}{V} \quad \text { or } \quad P V=n R T\] \[C_{P}=\left(\frac{\partial(E+P V)}{\partial T}\right)_{N, P}=\frac{5}{2} n R\] \[\gamma=C_{P} / C_{V}=\frac{5}{3}\] \[\mu \equiv\left(\frac{\partial E}{\partial N}\right)_{V, S}=E\left[\frac{5}{3 N}-\frac{2 S}{3 N^{2} k}\right]\] \[\mu=\frac{1}{N}[E+P V-T S] \equiv \frac{G}{N}\] \[\mu(N, V, T)=k T \ln \left\{\frac{N}{V}\left(\frac{h^{2}}{2 \pi m k T}\right)^{3 / 2}\right\}\] \[A=E-T S=G-P V=N k T\left[\ln \left\{\frac{N}{V}\left(\frac{h^{2}}{2 \pi m k T}\right)^{3 / 2}\right\}-1\right]\]微正则系综
超球体体积和表面积分别为
\[V_n(R)=\frac{\pi^{\frac{n}{2}} R^{n}}{\Gamma\left(\frac{n}{2}+1\right)}\] \[S_{n-1}(R)=\frac{nV_n}{R}\]对理想气体,对$q$积分得到$V^N$,剩下的即为对$p$形成的$3N$维超壳体求体积。 超壳体体积约等与半径平均值处的表面积乘以半径差值
\[V\simeq S_{n-1}(\bar{R})\delta R = \Delta\left(\frac{m}{2 E}\right)^{1 / 2}\left\{\frac{2 \pi^{3 N / 2}}{[(3 N / 2)-1] !}(2 m E)^{(3 N-1) / 2}\right\}\] \[\omega \simeq \frac{\Delta}{E} V^{N} \frac{(2 \pi m E)^{3_{N / 2}}}{[(3 N / 2)-1] !}\]若系统有$\Nu$个自由度,则 \(\omega_0=h^\Nu\)
对于单粒子,$\Nu=3$
\[\Sigma(P) \approx \frac{1}{h^{3}} \int_{p \leq P} \int\left(d^{3} q d^{3} p\right)=\frac{V}{h^{3}} \frac{4 \pi}{3} P^{3}\] \[g(p) d p=\frac{d \Sigma(p)}{d p} d p \approx \frac{V}{h^{3}} 4 \pi p^{2} d p\] \[\Sigma(E) \approx \frac{V}{h^{3}} \frac{4 \pi}{3}(2 m E)^{3 / 2}\] \[a(\varepsilon) d \varepsilon=\frac{d \Sigma(\varepsilon)}{d \varepsilon} d \varepsilon \approx \frac{V}{h^{3}} 2 \pi(2 m)^{3 / 2} \varepsilon^{1 / 2} d \varepsilon\]以上针对于无限大体系,对于有限体系,有修正
\[\Sigma(P) \simeq \frac{V}{h^{3}} \frac{4 \pi}{3} P^{3}+\theta \frac{S}{h^{2}} \frac{\pi}{4} P^{2}\] \[\Sigma(E) \simeq \frac{V}{h^{3}} \frac{4 \pi}{3}(2 m E)^{3 / 2}+\theta \frac{S}{h^{2}} \frac{\pi m E}{2}\]其中$-1\le \theta \le 1$,由边界处的波函数的边界条件决定
正则系综
\[H(q, p)=\sum_{i=1}^{N}\left(p_{i}^{2} / 2 m\right)\]对相空间积分
\[Q_{N}(V, T) =\frac{V^{N}}{N ! h^{3 N}}\left[\int_{0}^{\infty} e^{-p^{2} / 2 m k T}\left(4 \pi p^{2} d p\right)\right]^{N} =\frac{1}{N !}\left[\frac{V}{h^{3}}(2 \pi m k T)^{3 / 2}\right]^{N}\] \[A(N, V, T) \equiv-k T \ln Q_{N}(V, T)=N k T\left[\ln \left\{\frac{N}{V}\left(\frac{h^{2}}{2 \pi m k T}\right)^{3 / 2}\right\}-1\right] .\] \[\mu \equiv\left(\frac{\partial A}{\partial N}\right)_{V, T}=k T \ln \left\{\frac{N}{V}\left(\frac{h^{2}}{2 \pi m k T}\right)^{3 / 2}\right\}\] \[P \equiv-\left(\frac{\partial A}{\partial V}\right)_{N, T}=\frac{N k T}{V}\] \[S \equiv-\left(\frac{\partial A}{\partial T}\right)_{N, V}=N k\left[\ln \left\{\frac{V}{N}\left(\frac{2 \pi m k T}{h^{2}}\right)^{3 / 2}\right\}+\frac{5}{2}\right]\]与热力学与统计力学中的结论相同。
\[g(E)=\frac{\partial \Sigma}{\partial E} \approx \frac{1}{N !}\left(\frac{V}{h^{3}}\right)^{N} \frac{(2 \pi m)^{3 N / 2}}{\{(3 N / 2)-1\} !} E^{(3 N / 2)-1}\]对其积分,其实际上是一个Gamma函数(或等价于做一个拉普拉斯变换)
\[Q_{N}(\beta)=\frac{1}{N !}\left(\frac{V}{h^{3}}\right)^{N}\left(\frac{2 \pi m}{\beta}\right)^{3 N / 2}\]从单粒子出发
\[a(\varepsilon) \approx \frac{2 \pi V}{h^{3}}(2 m)^{3 / 2} \varepsilon^{1 / 2}\] \[Q_{1}(\beta)=\int_{0}^{\infty} e^{-\beta \varepsilon} a(\varepsilon) d \varepsilon=\frac{V}{h^{3}}\left(\frac{2 \pi m}{\beta}\right)^{3 / 2}\] \[Q_{N}(V, T)=\frac{1}{N !}\left[Q_{1}(V, T)\right]^{N}\]同样得到相同的表达式。
也可以利用反拉普拉斯变换从配分函数得到态密度。
巨正则系综
粒子可以处于空间任意位置 \(Q_{1}(V, T)=V f(T)\)
\[Q_{N}(V, T)=\frac{\left[Q_{1}(V, T)\right]^{N}}{N !},\] \[\mathcal{Q}(z, V, T) =\sum_{N_{r}=0}^{\infty} z^{N_{r}} Q_{N_{r}}(V, T)=\sum_{N_{r}=0}^{\infty} \frac{\{z V f(T)\}^{N_{r}}}{N_{r} !} =\exp \{z V f(T)\},\] \[q(z, V, T)=z V f(T)\] \[\begin{array}{l} P=z k T f(T), \\ N=z V f(T), \\ U=z V k T^{2} f^{\prime}(T), \\ A=N k T \ln z-z V k T f(T), \end{array}\] \[S=-N k \ln z+z V k\left\{T f^{\prime}(T)+f(T)\right\}\] \[U=N k T^{2} f^{\prime}(T) / f(T)\] \[C_{V}=N k \frac{2 T f(T) f^{\prime}(T)+T^{2}\left\{f(T) f^{\prime \prime}(T)-\left[f^{\prime}(T)\right]^{2}\right\}}{[f(T)]^{2}} .\]假定$f(T) \propto T^{n}$ \(U=n(N k T)\)
\[C_{V}=n(N k) .\]$n=3 / 2$ 时对应于非相对论性气体, 而 $n=3$ 时对应于极端相对论性气体.
本文由 joe_zhouman 创作,采用 知识共享署名4.0
国际许可协议进行许可
本站文章除注明转载/出处外,均为本站原创或翻译,转载前请务必署名
最后编辑时间为:2021-12-05 00:20:50
