对于迭代法求解线性方程的算法做了一个基本的总结
定常迭代法
原理
对于方程$Ax=b$
A可分解为$A = M-N$
迭代格式$Mx^{(k+1)}=Nx^{(k)}+b$
迭代法收敛: \(\Leftrightarrow \rho(M)<1 \Rightarrow ||M||<1\)
收敛速度
基本迭代法
对于基本迭代法,从另一方面,A可分解为$A = D+L+U$,其中
$D := diag(diag(A))$, 即为A的对角元组成的对角阵
$L := tril(A)-D$, 即为A的严格下三角阵(对角元为0)
$U := triu(A)-D$, 即为A的严格上三角阵(对角元为0.
以下列出的迭代法中$M$均可用以上的三个矩阵表示
常用基本迭代法
Jacobi method
\[M:=D\] \[x^{(k+1)}=-D^{-1}(L+U)x^{(k)}+D^{-1}b\] \[x^{(k+1)}_i = (b_i-\sum\limits_{j\ne i} a_{ij}x_j^{(k)})/a_{ii}\]收敛性
- 充要条件:$\rho(D^{-1}(L+U))<1$
- 充分条件:$a_{ii}>\sum\limits_{j\ne i}a_{ij}$,即A为严格对角占优矩阵
- 充分条件:$a_{ii}\ge\sum\limits_{j\ne i}a_{ij}$,即A为弱对角占优矩阵,且A为不可约矩阵
Damped (weighted) Jacobi method
\(M:=\frac{1}{\omega}D\) \(x^{(k+1)}=-D^{-1}((\omega-1)D+L+U)x^{(k)}+\omega D^{-1}b\) \(x^{(k+1)}_i = (1-\omega)x_i^{(k)}+ \omega(b_i-\sum\limits_{j\ne i} a_{ij}x_j^{(k)})/a_{ii}\)
收敛性
- $\rho(I-\omega D^{-1}A)\lt 1 \Leftrightarrow 0\lt \omega \lt 2/\rho(D^{-1}A)$
- 最小谱半径
\(\rho_{min} = 1-\frac{2}{cond(D^{-1}A)+1}\) \(when: \omega = \frac{2}{\lambda_{max}(D^{-1}A)+\lambda_{min}(D^{-1}A)}\) \(cond(A) =||A^{-1}||_p||A||_p\)
代码
function [x,err,kI] = Jacobi(A,b,N,err0,x0)
%JACOBI Jocobi迭代的迭代形式
narginchk(2,5);
if nargin < 5
x0 = zeros(size(b));
end
if nargin < 4
err0 = 1e-3;
end
if nargin < 3
N = 20;
end
x = x0;
n = length(b);
kI = 0;
err = 1;
while err > err0 && kI <N
for i = 1:n
s = 0;
for j = [1:i-1,i+1:n]
s = s + A(i,j)*x0(j);
end
x(i) = (b(i)-s)/A(i,i);
end
kI = kI + 1;
x0 = x;
err = norm(A*x-b);
end
Gauss-Seidel method
\(M:=D+L\) \(x^{(k+1)}=-(D+L)^{-1}Ux^{(k)}+(D+L)^{-1}b\) \(x^{(k+1)}_i = (b_i-\sum\limits_{j=1}^{i-1} a_{ij}x_j^{(k+1)} -\sum\limits_{j=i+1}^{n} a_{ij}x_j^{(k)})/a_{ii}\)
-
收敛性
- 充要条件:$\rho((D+L)^{-1}U)<1$
- 充分条件:$a_{ii}>\sum\limits_{j\ne i}a_{ij}$,即A为严格对角占优矩阵
- 充分条件:$a_{ii}\ge\sum\limits_{j\ne i}a_{ij}$,即A为弱对角占优矩阵,且A为不可约矩阵
-
充分条件:A为对称正定矩阵
- 代码
function [x0,err,kI] = GaussSeidel(A,b,N,err0,x0)
%GaussSeidel 高斯-赛德尔迭代的迭代形式
narginchk(2,5);
if nargin < 5
x0 = zeros(size(b));
end
if nargin < 4
err0 = 1e-3;
end
if nargin < 3
N = 20;
end
err = norm(A*x0-b);
kI = 0;
n = length(x0);
while err > err0 && kI < N
for i = 1:n
s = 0;
for j = [1:i-1,i+1:n]
s = s + A(i,j)*x0(j);
end
x0(i)=(b(i)-s)/A(i,i);
end
err = norm(A*x0-b);
kI = kI + 1;
end
end
Successive over-relaxation (SOR) method
\(M:=\frac{1}{\omega}D+L\) \(x^{(k+1)}=-(\frac{1}{\omega}D+L)^{-1}((1-\frac{1}{\omega})D+U)x^{(k)}+ (\frac{1}{\omega}D+L)^{-1}b\) \(x^{(k+1)}_i =(1-\omega)x_i^{(k)}+\omega(b_i-\sum\limits_{j=1}^{i-1} a_{ij}x_j^{(k+1)} -\sum\limits_{j=i+1}^{n} a_{ij}x_j^{(k)})/a_{ii}\)
-
收敛性
- 充要条件:$\rho((D+\omega L)^{-1}((\omega -1)D+\omega U))<1$
-
充分条件:A为对称正定矩阵且$0<\omega<2$
- 收敛速度
假定满足
- $0<\omega<2$
- $D^{-1}(L+U)$ 仅有实特征值
- Jacobi方法收敛,及$\mu := \rho(D^{-1}(L+U))<1$
- $det(A)\ne 0$
则收敛速度 \(\rho = (\omega\mu+\sqrt{\omega^2\mu^2-4(\omega-1)^2})^2/2, 0\lt \omega\le\omega_{opt}\) \(\rho = \omega-1, \omega_{opt}\le\omega<2\) 其中 \(\omega_{opt}=1+\left(\frac{\mu}{1+\sqrt{1-\mu^2}} \right)^2\)
- 代码
function [x0,err,kI] = SOR(A,b,omega,N,err0,x0)
%SOR 逐次超松弛迭代
% 此处显示详细说明
narginchk(3,6);
if nargin < 6
x0 = zeros(size(b));
end
if nargin < 5
err0 = 1e-3;
end
if nargin < 4
N = 20;
end
kI = 0;
err = 1;
n = length(b);
x = x0;
while err > err0 && kI < N
for i = 1:n
s = 0;
for j = 1:i-1
s = s+A(i,j)*x(j);
end
for j = i+1:n
s = s+A(i,j)*x0(j);
end
% x(i)=(1-omega)*x0(i)+omega/A(i,i)*(b(i)-s);
x(i)=x0(i)+omega*((b(i)-s)/A(i,i)-x0(i));
% 相对上面的写法,少一次乘法计算。
end
err = norm(x-x0);
x0 = x;
kI = kI+1;
end
end
Accelerated Overrelaxation (AOR) Method
\(M:=(1-\omega)I-\omega(D+rL)^{-1}((1-r)L+U)\) \(x^{(k+1)}=(1-\omega)Ix^{(k)}-\omega(D+rL)^{-1}((1-r)L+U)x^{(k)}+\omega(D+rL)^{-1} b\) \(x^{(k+1)}_i=(1-\omega)x^{(k)}_i+(\omega b-\sum\limits_{j=1}^{i-1}(ra_{ij}x^{(k+1)}_j+ (\omega-r)x_j^{(k)})-\sum\limits_{j = i+1}^n\omega a_{ij}x^{(k)}_j)\)
- 收敛性
Symmetric successive over-relaxation (SSOR) method
\[M:=\frac{1}{\omega(2-\omega)}(D+\omega L)D^{-1}(D+\omega U)\]适用于对称矩阵
(Modified) Richardson method
\(M:=\frac{1}{\omega}I\) \(x^{(k+1)}=-(\omega A-I)x^{(k)}+\omega b =x^{(k)}+\omega(b-Ax^{(k)})\) \(x^{(k+1)}_i=x^{(k)}_i+\omega(b_i-\sum\limits_{j=1}^na_{ij}x_j^{(k)})\)
- 收敛性
- 代码
function [x0,err,kI] = AOR(A,b,omega,r,N,err0,x0)
%AOR Accelerated Overrelaxation Method迭代形式
% 此处显示详细说明
narginchk(4,7);
if nargin < 7
x0 = zeros(size(b));
end
if nargin < 6
err0 = 1e-3;
end
if nargin < 5
N = 20;
end
kI = 0;
err = 1;
n = length(b);
x = x0;
while err > err0 && kI < N
for i = 1:n
s1 = 0;
s2 = 0;
s3 = 0;
for j = 1:i-1
s1 = s1+A(i,j)*x(j);
s2 = s2 + A(i,j)*x0(j);
end
for j = i+1:n
s3 = s3+A(i,j)*x0(j);
end
x(i)=x0(i)+omega*((b(i)-s2-s3)/A(i,i)-x0(i))+r*(s2-s1)/A(i,i);
% 以上写法增加了两个辅助中间量,减小了总体的乘法运算数量
end
err = norm(A*x-b);
x0 = x;
kI = kI+1;
end
end
泛函优化方法
原理
对泛函 \(f(\mathbf{x})=\frac12(\mathbf{x^T}A\mathbf{x})-\mathbf{x^T}b\) \(\nabla f = \mathbf{Ax-b}\) \(\nabla^2f = \mathbf{A}\) 将其看做一个优化问题,由于A为正定矩阵,则当$f(\mathbf{x})$取最小值时,有$\mathbf{Ax-b=0}$
最速下降法
适用于实正定对称矩阵,对于一些非正定矩阵,可以转化为等价问题$\mathbf{A^{T}Ax-A^{T}b=0}$

代码
function [x,r,kI] = GD(A,b,N,err0,x)
%GD Gradient Descent method 最速下降法
% 此处显示详细说明
narginchk(2,5);
n = length(b);
if nargin < 5
x = zeros(size(b));
end
if nargin < 4
err0 = 1e-3;
end
if nargin < 3
N = n;
end
r = b-A*x;
kI = 0;
while norm(r) > err0 && kI < N
% a = r'*r/(r'*A*r);
% x = x + a*r;
% r = b-A*x;
% 为了避免在一次循环中计算两次A的乘积
t = A*r;
a = r'*r/(r'*t);
x = x+a*r;
r = r-a*t;
kI = kI + 1;
end
end
Krylov子空间方法
原理
考虑一系列向量${\mathbf{b, Ab, A^2b, …, A^nb}}$, 其属于一个n维空间(n为A的阶数),则这n+1个向量一定线性相关。 即$\exists \alpha_0, \alpha_1, …, \alpha_n$,使得 \(\alpha_0\mathbf{b}+\alpha_1\mathbf{Ab}+...+\alpha_n\mathbf{A^nb}=0\) 令k为满足$\alpha_k\ne0$的最小整数,则 \(\mathbf{x=A^{-1}b}=-\frac{1}{\alpha_k}(\alpha_{k+1}\mathbf{b}+...+\alpha_n\mathbf{A^{n-k-1}b})\)
一些具体方法
共轭梯度法
无舍入误差时,可作为直接法。实际均用作迭代法 适用于实正定对称矩阵
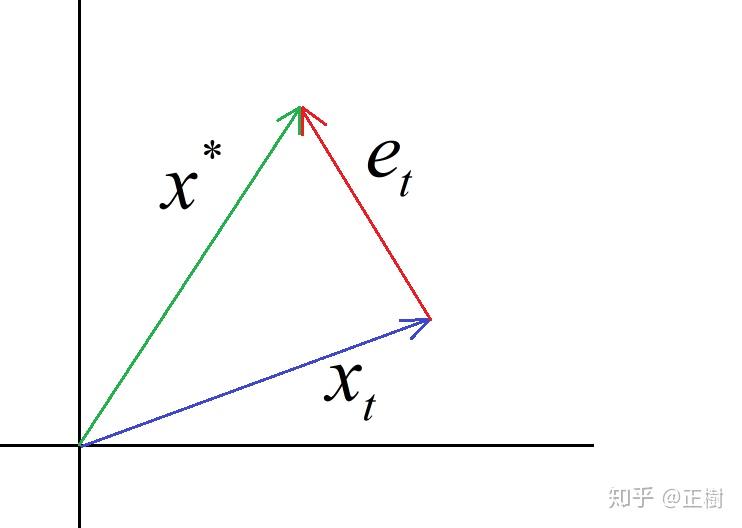
核心思想:当前的误差跟上一步的方向正交, 意味着这个方向彻底走到了极致 (偏小或偏大都会导致误差变大)
代码
function [x,r,kI] = CG(A,b,N,err0,x)
%CG Conjugate gradient method 共轭梯度法
% 此处显示详细说明
narginchk(2,5);
n = length(b);
if nargin < 5
x = zeros(size(b));
end
if nargin < 4
err0 = 1e-3;
end
if nargin < 3
N = n;
end
if N > n
warning("最大迭代步数%d大于矩阵的阶数%d,最大步数重新设置为矩阵的阶数",N,n);
N = n;
end
r = b-A*x;
p = r;
for kI=1:N
a = r'*p/(p'*A*p);
x = x+a*p;
r = r - a*A*p;
if norm(r)<err0
break;
end
b = -r'*A*p/(p'*A*p);
p = r + b*p;
end
end
预调试共轭梯度法
通过预调试使算法更快的收敛 具体做法为在每一次计算p,$\alpha$和$\beta$时,用$M^{-1}r$替代$r$($r^T$不做改变)。$M$即为预调试子。
柔性预调试共轭梯度法
与上面的算法相比,在计算$\beta$时,使用如下计算式替代: \(\beta_k := \frac{r_k^T(z_{k+1}-z_k)}{r^T_kz_k}\)
Biconjugate gradient stabilized (BiCGSTAB) Method
代码
function [x,r,kI] = BiCGSTAB_T(A,b,M1,M2,N,err0,x)
%BiCGSTAB_T Biconjugate gradient stabilized method
%% Details
% This algorithm does not require the matrix A to be self-adjoint, i.e.,
% $A^H=A$ is not required.
%
%% Syntax:
% * [x,r,kI] = BiCGSTAB_T(A,b,M1,M2)
% * [x,r,kI] = BiCGSTAB_T(A,b,M1,M2,N)
% * [x,r,kI] = BiCGSTAB_T(A,b,M1,M2,N,err0)
% * [x,r,kI] = BiCGSTAB_T(A,b,M1,M2,N,err0,x)
%
%% Inputs:
% * *A* - parameter matrix of $Ax=b$, must be square matrix .
% * *b* - $Ax=b$ must be column vector, and rank(A) = length(b).
% * *M1* - preconditioner $K = K_1K_2\approx A$, $M1=K^{-1}$
% * *M2* - preconditioner $M2 = K1^{-1}$
% * *N* - The maximum iteration step. Iteration will stop when steps meet
% N. Must be positive integer.
% * *err0* - Allowable error. Iteration will stop when the error is
% smaller than err0.
% * *x* - Initial guess of the answer.
%
%% Outputs:
% * *x* - The approximate solution of $Ax=b$ when steps or error meet the
% ending condition.
% * *r* - The error of the approximate solution. $err = x^*-x=x*-A^{-1}b$
% * *kI* - Iteration steps.
% * *
%% Example:
% # Line 1 of example
% # Line 2 of example
% # Line 3 of example
% # Line 4 of example
%
%% Dependence
% # Other m-files required: none
% # Subfunctions: none
% # MAT-files required: none
% # See Also :
% * ./+Preconditioning
%
%% TODO
% * use mex
narginchk(4,7);
n = length(b);
if nargin < 7
x = zeros(size(b));
end
if nargin < 6
err0 = 1e-3;
end
if nargin < 5
N = n;
end
r = b - A*x;
rb = r; %% an arbitrary vector such that (rb,r)!=0;
rho0 = 1;a = 1;w = 1;
v = zeros(size(b));p = zeros(size(b));
for kI = 1:N
rho = rb'*r;
beta = rho/rho0*a/w;
p = r + beta*(p-w*v);
y = M1*p;
v = A*y;
a = rho/(rb'*v);
h = x+a*y;
if norm(r)<err0
x = h;
break;
end
s = r - a*v;
z = M1*s;
t = A*z;
w = (M2*t)'*(M2*s)/((M2*t)'*(M2*t));
x = h+w*z;
if norm(r) < err0
break;
end
r = s-w*t;
rho0 = rho;
end
end
小结
迭代法的选取
效率最高的显然是共轭梯度法,matlab自己也有封装。
对称矩阵与一般矩阵的关系
以上有几种方法只适用于对称矩阵,但对一个一般的方程$Ax=b$, 可求其等价方程$A^TAx=A^Tb$, $A^TA$为对称矩阵。
附录
A. 对角占优矩阵
B. 正定矩阵
C. (不)可约矩阵
D. 谱半径
E. 条件数
F. 预调试
本文由 joe_zhouman 创作,采用 知识共享署名4.0
国际许可协议进行许可
本站文章除注明转载/出处外,均为本站原创或翻译,转载前请务必署名
最后编辑时间为:2021-11-21 17:13:05
