波动方程解

博客分类: code
傅里叶分析 (2) matlab (7)

波动方程解

傅里叶分析 (2) matlab (7)

波动方程的两种解法可视化

波动方程

波动方程主要用以描述自然界中的各种的波动现象。

二维平面波动方程形式如下：

\[\large\frac{\partial^2u}{\partial t^2} = \frac{\partial^2u}{\partial x^2} \quad on \quad 0 \le x\le \pi, \quad with \quad t\ge0\]

注：上述方程将系数简化为一，不是标准的波动方程

行波解

简述

行波 是波的一种传播状态，因其好像在往某个方向移动而得名。

行波的方程可表示为

右行波方程

\[\large u(x,t)=F(x+t)\]

左行波方程

\[\large u(x,t)=F(x-t)\]

则行波形式的方程为

\[\large u(x,t)=F(x+t)+G(x-t)\]

此方程的通解为

\[\large u(x,t)=\frac{1}{2}[f(x+t)+f(x-t)]+\frac{1}{2}\int_{x-t}^{x+t}g(y)dy\]

上述解也被称为达朗贝尔公式

特解

在达朗贝尔公式中，取

\[\large f(x)=2\sin x,\quad g(x) = 4\cos 2x\] \[\large u(x,t)=\sin (x+t)+\sin (x-t)+\sin 2(x+t) - \sin 2(x-t)\] \[\large F(x+t)=\sin (x+t)+\sin 2(x+t)\]

S\(\large G(x-t)=\sin (x-t)-\sin 2(x-t)\)

代码

clc,clear,close all

x = -pi:0.1:3*pi;

t = 0;

y = sin(x+t) + sin(x-t)+sin(2*x+2*t)-sin(2*x-2*t);
y1 = sin(x+t)+sin(2*x+2*t);
y2 = sin(x-t)-sin(2*x-2*t);
wave = plot(x,y,'linewidth',1);
hold on
wave1 = plot(x,y1,'linewidth',1);

wave2 = plot(x,y2,'linewidth',1);
legend("合成波","左行波","右行波","fontname","宋体")
ylim([-4,4])
for t = 0:0.1:6*pi
    ydata = sin(x+t) + sin(x-t)+sin(2*x+2*t)-sin(2*x-2*t);
    ydata1 = sin(x+t)+sin(2*x+2*t);
    ydata2 = sin(x-t)-sin(2*x-2*t);
    set(wave,'ydata',ydata);
    set(wave1,'ydata',ydata1);
    set(wave2,'ydata',ydata2);
    drawnow
end

结果

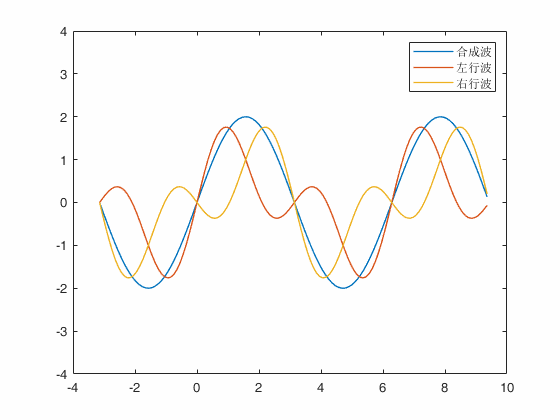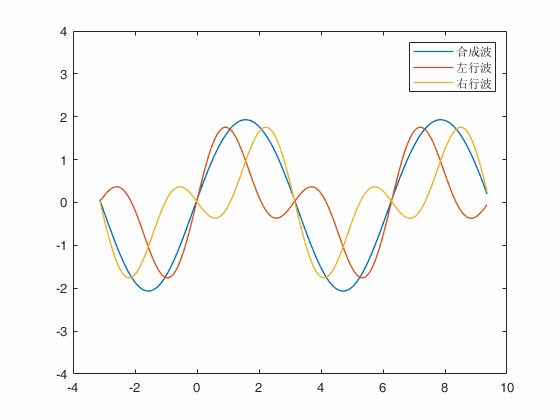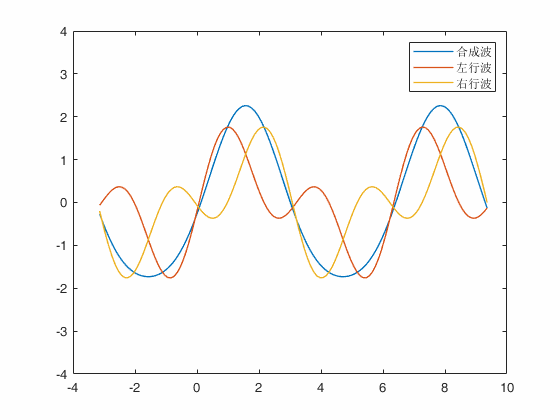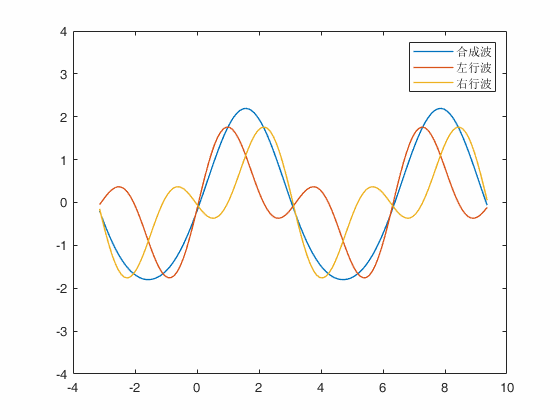
驻波解

简述

驻波 波节和波腹的位置始终是不变的，给人“驻立不动”的印象。

驻波可表示为

\[\large u(x,t)=\varphi(x)\psi(t)\]

其通解为

\[\large u(x,t) = \sum ^{\infty}_{m=1}(A_m \cos mt + B_m \sin mt)\sin mx\]

代码

clc,clear,close all
x = -pi:0.1:3*pi;

t = 0;

y1 = cos(x)*sin(t);
y2 = sin(x)*sin(t);
y = y1+y2;

wave = plot(x,y,'linewidth',1);
hold on
wave1 = plot(x,y1,'linewidth',1);

wave2 = plot(x,y2,'linewidth',1);
legend("合成波","驻波1","驻波2","fontname","宋体")
ylim([-4,4])
for t = 0:0.1:6*pi
    ydata1 = cos(x)*sin(t);
    ydata2 = sin(x)*sin(t);
    ydata = ydata1.*ydata2;
    set(wave,'ydata',ydata);
    set(wave1,'ydata',ydata1);
    set(wave2,'ydata',ydata2);
    drawnow
end

结果

本文由 joe_zhouman 创作，采用 知识共享署名4.0 国际许可协议进行许可
本站文章除注明转载/出处外，均为本站原创或翻译，转载前请务必署名
最后编辑时间为:2021-03-09 17:54:39